数学高考圆锥曲线_数学高考圆锥曲线大题多少人可以做

1.高三数学圆锥曲线题，请高手解答，多谢！

在每年的高考中,有关圆锥曲线的试题约占全卷总分的13%，是相当重要的考点。下面我整理了《高中数学圆锥曲线公式大全》，欢迎阅读。

　高中数学圆锥曲线公式大全

1.焦半径公式 ，P为椭圆上任意一点，则│PF1│= a + eXo

│PF2│= a - eXo

F1 F2分别为其左，右焦点

2.通径长 = 2b?/a

3.焦点三角形面积公式

S⊿PF1F2 = b?tanθ/2 θ为∠F1PF2

这个可能有点难理解，不过结合第一定义可以较快的推，双曲线的也是同样方法

4.左准点Q 自己取的名字方便叙述，准线与X轴的焦点

过左焦点F1的任意一条线与椭圆交与A ，B 那么一定有：X轴平分∠AQB

在右边也是一样

1.通径就不说了 2.焦半径公式有8个，很难打符号的，不过可以根据极座标方程来直接解答，比焦半径公式还快一些

3.焦点三角形面积公式

S⊿PF1F2 =b?cotθ/2 左右支都是它

y?=2px p>0过焦点的直线交它于AX1,Y1,BX2,Y2两点

1.│AB│=X1 + X2 + p =2p/sin?θ θ为直线AB的倾斜角

2. Y1*Y2 = -p? ， X1*X2 = p?/4

3.1/│FA│ + 1/│FB│ = 2/p

4.结论：以AB 为直径的圆与抛物线的准线线切

5.焦半径公式： │FA│= X1 + p/2 = p/1-cosθ

直线与圆锥曲线 y= Fx 相交于A ，B，则

│AB│=√1+k? * [√Δ/│a│]

圆锥曲线包括椭圆圆为椭圆的特例，抛物线，双曲线。

圆锥曲线二次曲线的统一定义：

到定点焦点的距离与到定直线准线的距离的商是常数e离心率的点的轨迹。当e>1时，为双曲线的一支，当e=1时，为抛物线，当0

有途网我建议还是先研究书本的基本概念，掌握相关公式，图形特点，利用这些概念解决题目，之后再做习题。

高中数学主要考点及易错点整理

高中数学易错点

不等式

1.利用均值不等式求最值时，你是否注意到：“一正;二定;三等”.

2.绝对值不等式的解法及其几何意义是什么?

3.解分式不等式应注意什么问题?用“根轴法”解整式分式不等式的注意事项是什么?

4.解含引数不等式的通法是“定义域为前提，函式的单调性为基础，分类讨论是关键”，注意解完之后要写上：“综上，原不等式的解集是……”.

5.在求不等式的解集、定义域及值域时，其结果一定要用 *** 或区间表示;不能用不等式表示.

6.两个不等式相乘时,必须注意同向同正时才能相乘,即同向同正可乘;同时要注意“同号可倒”即a>b>0，a<0.

　高中数学易错点

数列

1.解决一些等比数列的前项和问题，你注意到要对公比及两种情况进行讨论了吗?

2.在“已知，求”的问题中,你在利用公式时注意到了吗?时，应有需要验证，有些题目通项是分段函式。

3.你知道存在的条件吗?你理解数列、有穷数列、无穷数列的概念吗?你知道无穷数列的前项和与所有项的和的不同吗?什么样的无穷等比数列的所有项的和必定存在?

4.数列单调性问题能否等同于对应函式的单调性问题?数列是特殊函式，但其定义域中的值不是连续的。

5.应用数学归纳法一要注意步骤齐全，二要注意从到过程中，先假设时成立，再结合一些数学方法用来证明时也成立。

高中数学主要考点：立体几何初步

考点1：空间几何体的结构、三检视和直检视

考点2：空间几何体的表面积和体积

考点3：点、线、面的位置关系

考点4：直线、平面平行的性质与判定

考点5：直线、平面垂直的判定及其性质

高中数学主要考点：三角函式

考点1：任意角的三角函式、同三角函式和诱导公式

考点2：三角函式的影象和性质

考点3：三角函式的最值与综合运用

考点4：三角恒等变换

考点5：解三角形

高中数学主要考点：数列

考点1：数列的概念及其表示

考点2：等差数列

考点3:等比数列

考点4：数列的综合运用

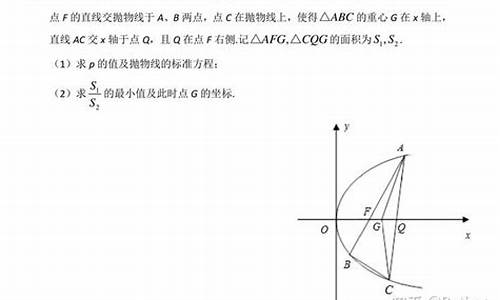
高三数学圆锥曲线题，请高手解答，多谢！

很多朋友或同学们并不懂积分。所以，在下用合理的逻辑，做简单的解释，具备初高中数学都可理解。如下：

首先给个圆柱，高H，底半径R（H与R非无穷大）。

然后，以它的底和高为基础在内部做个圆柱。

怎么比较二者体积呢？关键时刻来了

这里我们先给定几个定义，

1， 假定上帝存在；

2， 用上帝之刀平行于圆柱底均匀切割N次，使N无穷大，得到（N+1）个圆柱和圆锥的切面, 切面的厚度为H/（N+1）；

3， 无穷切, 使N无穷大到某程度，得到 Δr= R/N ,使得Δr为圆锥的元点半径（不能更小，类 似电子电荷（元电荷）电量）。这是逻辑上的关键，请深刻理解。

理解了以上定义，我们就可以知道相关计算数据了。对于圆锥的所有切面而言，

各切面半径从顶到底依次为0，Δr，2Δr，…mΔr，…NΔr=R（ 因为Δr已定义不可再分），

圆锥各切面面积从顶到底依次为0，πΔr^2,π(2Δr)^2……π（NΔr)^2，

各单切面体积依次是 切面面积*(H/(N+1))

故圆锥体积等于所有切面的体积加和

V锥=（πΔr^2）*(0+1+2^2+3^2+...+N^2) * (H/(N+1))

我们再来看看圆柱的体积。它是(N+1)个圆柱切面体积的加和，很简单

V柱=(N+1) * （πR^2）*（H/(N+1)）=(N+1) *（π（NΔr)^2）*（H/(N+1)）

故 V锥/ V柱=(0+1+2^2+3^2+...+N^2) / ((N^2)*(N+1))

根据数列知识，

V锥/ V柱=N*(N+1)*(2N+1)/6 / ((N^2)*(N+1))=1/3+1/(6 N)

故，N为无穷大时，V锥/ V柱=1/3

抛物线x^2=4y的焦点坐标是F(0,1),即有椭圆的c=1.又有A(0,2),即有a=2, b^2=a^2-c^2=4-1=3

故椭圆E方程是y^2/4+x^2/3=1.

设过F(0,1)的直线方程是y=kx+1.代入到抛物线中有x^2=4(kx+1)

即有x^2-4kx-4=0

设C坐标是(x1,y1),D(x2,y2)

y=x^2/4, y'=x/2,则有L1的斜率k1=x1/2, L2的斜率k2=x2/2

故有k1*k2=x1x2/4=-4/4=-1

故有L1和L2垂直.

y=kx+1代入到椭圆中有(kx+1)^2/4+x^2/3=1,即有4x^2+3(k^2x^2+2kx+1)=12

(4+3k^2)x^2+6kx-9=0

设M坐标是(x3,y3),N(x4,y4),则有x3+x4=-6k/(4+3k^2),x3x4=-9/(4+3k^2)

又有S(AMN)=1/2AF*|X3-X4|=1/2*1*|x3-x4|=1/2根号[(x3+x4)^2-4x3x4]=1/2根号[36k^2/(4+3k^2)+36/(4+3k^2)]=1/2根号(36k^2+144+108k^2)/(4+3k^2)^2=1/2*12/(4+3k^2)*根号(k^2+1)=6根号(k^2+1)/(3k^2+4)

设t=根号(k^2+1)>=1,则有S=6t/(3t^2+1)=6/(3t+1/t)<=6/ (3+1)=3/2

即当根号(k^2+1)=1,即k=0时取得最大值是3/2.