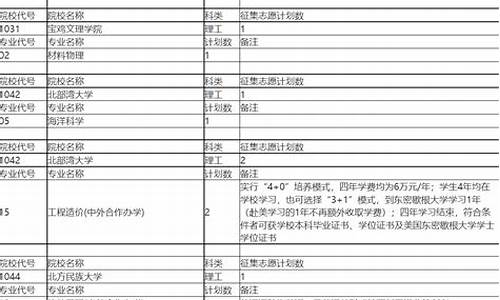
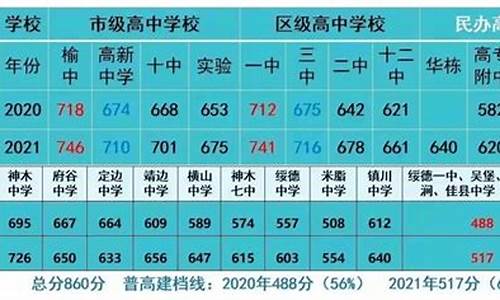
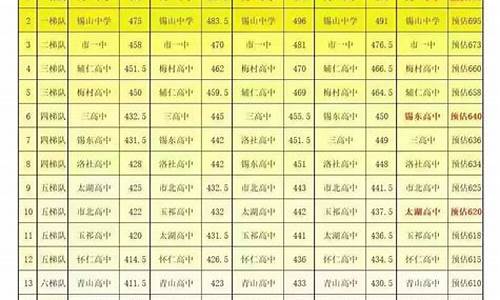
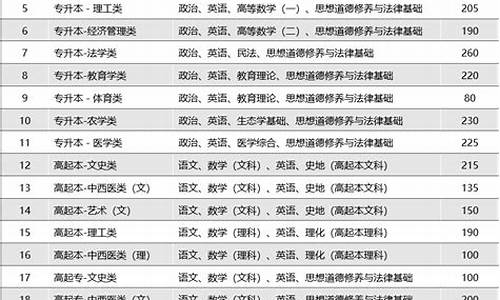
您现在的位置是: 首页 > 招生信息 招生信息
数学数列高考例题-高考数学数列经典题型及答案
tamoadmin 2024-10-31 人已围观
简介1.在高考数学中,如果考生从1开始加,直到30,那么2.高中数列数学题,急急急。3.问一道高二数学题(与数列有关)4.求高中数学数列用倒序相加法,裂项法,合并法求和的例题RT!在高考数学中,如果考生从1开始加,直到30,那么每次相加到最后是:103741824分=1037418.24元由题可知,为一个首项是1,公比是2,项数是30的一个等比数列。等比数列前n项和公式为:?1、Sn=n*a1(q=1
1.在高考数学中,如果考生从1开始加,直到30,那么
2.高中数列数学题,急急急。
3.问一道高二数学题(与数列有关)
4.求高中数学数列用倒序相加法,裂项法,合并法求和的例题RT!
在高考数学中,如果考生从1开始加,直到30,那么

每次相加到最后是:103741824分=1037418.24元
由题可知,为一个首项是1,公比是2,项数是30的一个等比数列。
等比数列前n项和公式为:?
1、Sn=n*a1(q=1)?
2、Sn=a1(1-q^n)/(1-q)?
=(a1-a1q^n)/(1-q)?
=a1/(1-q)-a1/(1-q)*q^n ( 即a-aq^n)
(前提:q不等于 1)
注意:以上n均属于正整数。
扩展资料:等比数列性质
1、若(an)为等比数列且各项为正,公比为q,则(log以a为底an的对数)成等差,公差为log以a为底q的对数。
2、等比数列前n项之和Sn=A1(1-q^n)/(1-q)=A1(q^n-1)/(q-1)=(A1q^n)/(q-1)-A1/(q-1)
在等比数列中,首项A1与公比q都不为零。
注意:上述公式中A^n表示A的n次方。
3、由于首项为a1,公比为q的等比数列的通项公式可以写成an=(a1/q)*q^n,它的指数函数y=a^x有着密切的联系,从而可以利用指数函数的性质来研究等比数列。
参考资料:百度百科-等比数列高中数列数学题,急急急。
解:
(1)
设{an}公差为d,则d≠0。设{bn}公比为q
a2=b2,a1+d=b1q
a1=b1=1代入,得d+1=q
d=q-1
d≠0,则q≠1
a8=b3,a1+7d=b1q?
a1=b1=1代入,得7d+1=q?
d=(q?-1)/7
q-1=(q?-1)/7
整理,得q?-7q+6=0
(q-1)(q-6)=0
q=1(舍去)或q=6
d=q-1=6-1=5
数列{an}的公差为5,数列{bn}的公比为6。
(2)
an=a1+(n-1)d=1+5(n-1)=5n-4
bn=b1q=1·6=6
数列{an}的通项公式为an=5n-4,数列{bn}的通项公式为bn=6。
(3)
Sn=(a1+an)n/2=(1+5n-4)n/2=n(5n-3)/2
Tn=b1(q?-1)/(q-1)=1·(6?-1)/(6-1)=(6?-1)/5
数列{an}的前n项和为n(5n-3)/2,数列{bn}的前n项和为(6?-1)/5。
问一道高二数学题(与数列有关)
cn=an/bn
=(4n-2)/[2/4^(n-1)]
=(2n-1)4^(n-1)
cn=(2n-1)4^(n-1)
Pn=(2n-1)4^(n-1)+(2n-3)4^(n-2)+(2n-5)4^(n-3)+……+5*4^2+3*4^1+4^0
4Pn=(2n-1)4^n+(2n-3)4^(n-1)+(2n-5)4^(n-2)+……+5*4^3+3*4^2+4^1
两式相减:
-3Pn=-(2n-1)4^n+2*4^(n-1)+2*4^(n-2)+……+2*4^3+2*4^2+2*4^1+1
=-(2n-1)4^n+2[4^(n-1)+4^(n-2)+……+4^3+4^2+4^1]+1
=-(2n-1)4^n+2*4[4^(n-1)-1]/(4-1)+1
=-(2n-1)4^n+(8/3)*4^(n-1)-5/3
=-(2n-1)4^n+(2/3)*4^n-5/3
=-(2n-5/3)4^n-5/3
Pn=(1/9)(6n-5)4^n+5/9
求高中数学数列用倒序相加法,裂项法,合并法求和的例题RT!
1.倒叙相加法:最基本的1+2+3+4……+100=(1+100)+(2+99)+(3+98)...(48+53)+(49+52)+(50+51)=101*50=5050稍微复杂的f{x}=1/[2^x+√2]求f[-5]+f{-4}+……+f{0}+……+f{5}+f{6}的值所以S=f(-5)+f(-4)+……+f(0)+……+f(5)+f(6)S=[f(-5)+f(6)]+[f(-4)+f(5)]+[f(-3)+f(4)]+[f(-2)+f(3)]+[f(-1)+f(2)]+[f(0)+f(1)]而f(-5)+f(6)...f(0)+f(1)等式子都满足f(x)+f(1-x)的形式也即使f(-5)+f(6)...f(0)+f(1)的值都是√2/2所以S=6×√2/2=3√22.裂项法这是分解与组合思想在数列求和中的具体应用.裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的.通项分解(裂项)如:(
1)1/n(n+1)=1/n-1/(n+1)(
2)1/(2n-1)(2n+1)=1/2[1/(2n-1)-1/(2n+1)] (3)1/n(n+1)(n+2)=1/2[1/n(n+1)-1/(n+1)(n+2)] (4)1/(√a+√b)=[1/(a-b)](√a-√b) (5)
n·n!=(n+1)!-n!简单的1.求数列an=1/n(n+1)
的前n项和.设
an=1/n(n+1)=1/n-1/(n+1)
(裂项)
则
Sn=1-1/2+1/2-1/3+1/4…+1/n-1/(n+1)(裂项求和)
=
1-1/(n+1) =
n/(n+1)复杂的3.合并法